142 Engineering Fundamentals
Resistance
Resistance is the opposition to current fl ow.
Resistors are used to limit current fl ow and
divide voltage. All conductors, components,
and circuits have some level of resistance. Resis-
tance is measured in ohms. The Greek symbol for
omega (Ω) is used to represent ohms.
Materials with very little resistance (allow
current to fl ow freely) are conductors. Copper,
aluminum, gold, and silver are examples of good
conductors. Materials with a very high resis-
tance that do not allow current to fl ow are called
insulators. Plastic, glass, rubber, and paper are
examples of good insulators.
A standard kitchen faucet can help you
understand the relationship between current,
voltage, and resistance. Think of the water pres-
sure as voltage, the amount of water fl owing as
current, and the faucet handle as providing resis-
tance. In this example, the water pressure (volt-
age) remains constant as it is supplied from the
water system. If the water is turned on as far as
possible, there is very little resistance from the
faucet and, therefore, very high fl ow (current).
By slowly turning the faucet handle, resistance
is increased and fl ow (current) is decreased. This
example shows that if voltage is held constant,
current and resistance are inversely proportional.
If resistance increases, current decreases. If resis-
tance decreases, current increases.
Power
Power can be defi ned as the rate at which
work is done or the amount of work done based
on a period of time. Electrical power can be
defi ned as the product of voltage and current. The
watt is the unit of electrical power. It is named
for the inventor of the steam engine, James Watt.
One watt is the measure of one volt moving one
coulomb of electricity in one second.
Laws
Ohm’s law is the relationship between resis-
tance, current, and voltage in electrical circuits.
This law is one of the most important concepts
to master in the fi eld of electrical engineering
because it will be used more than any other.
Ohm’s law was named for a nineteenth century
German physicist named Georg Ohm. He discov-
ered that if he kept resistance constant and varied
voltage, dividing the voltage by the current
always equaled the resistance. This formula can
be used to solve for any of the three variables:
R = E / I
I = E / R
E = I × R
For example, let’s say you want to calculate
the resistance of a fl ashlight bulb. You know that
your batteries are providing 3 V and you are
drawing 0.1 A (or 100 milliamps) of current fl ow.
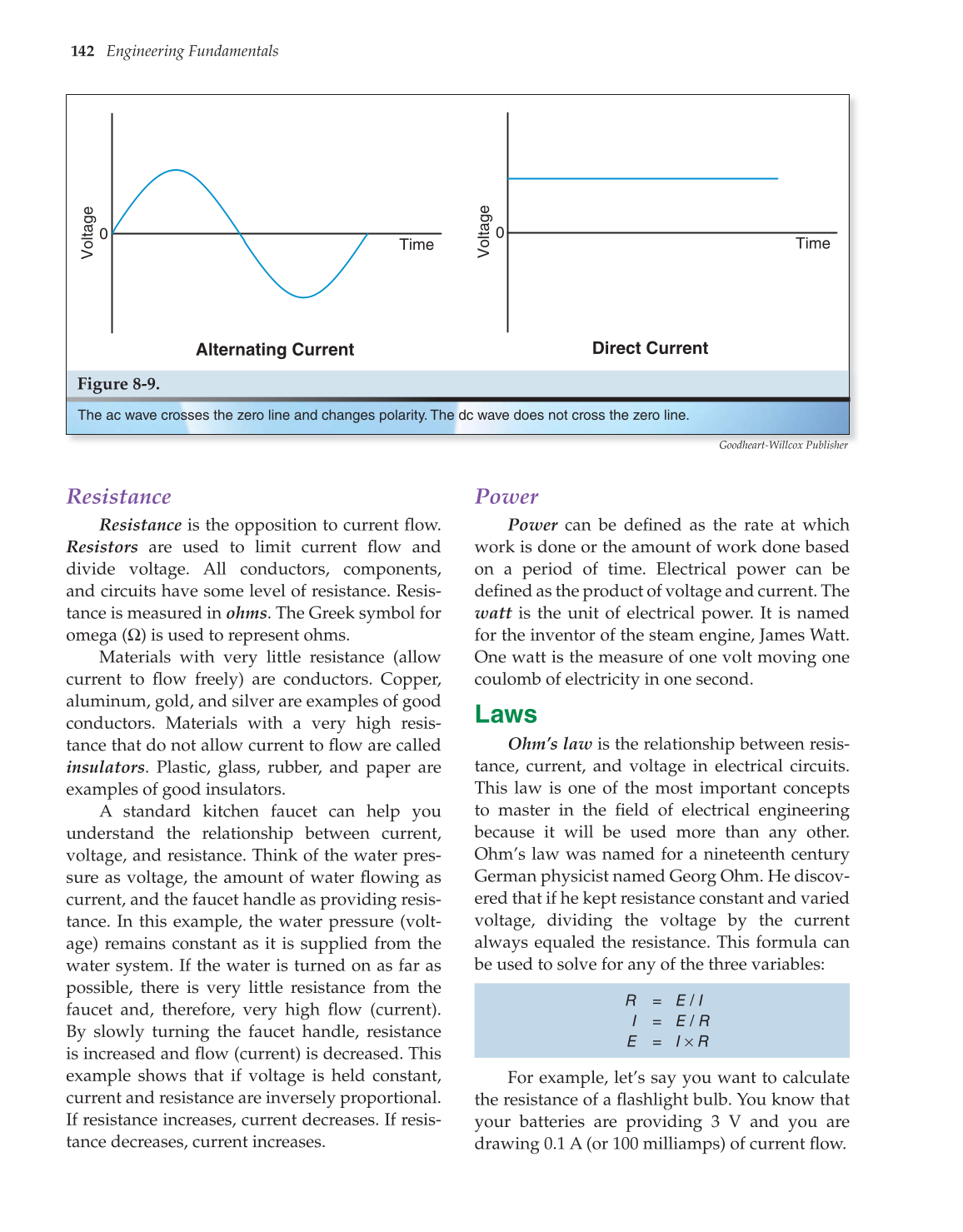
Figure 8-9.
The ac wave crosses the zero line and changes polarity. The dc wave does not cross the zero line.
0
Voltage
Voltage
Time Time
Alternating Current
Direct Current
0
Goodheart-Willcox Publisher